Oil Wildcatter, Raiffa (1968), Shenoy (1992)
In this example, an oil wildcatter must decide either to drill or not to drill. He is uncertain whether the hole is dry, wet or soaking in oil. The wildcatter can make seismic soundings that will help determine the geological structure of the site. The soundings will give a closed reflection pattern (indication for much oil), an open pattern (indication for some oil) or a diffuse pattern (almost no hope for oil).
The wildcatter has two decisions to make, namely whether to test with seismic soundings costing K$10 and whether to drill costing K$70. The utility gained from drilling is determined by the state of the hole (dry, wet or soaking). The reward of drilling a dry hole is zero, a wet hole is 120, and a soaking hole is 270.
The domain of this problem is modeled by the (limited-memory) influence diagram (LIMID) in Figure 1. Note the link from Seismic to Drill. It specifies that when the decision of Drill has to be made, the state of Seismic is known. If this link is not specified, the computations will be made under the assumption that this observation is not known by the decision maker when she has to make the drill decision.
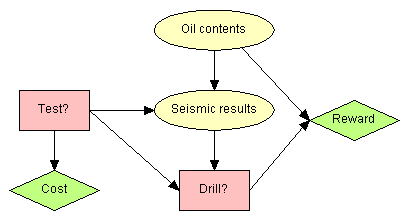
Figure 1: The Oil Wildcatter problem as an influence diagram.
Figure 1 above shows the Oil Wildcatter problem as an influence diagram. The influence diagram
Assume the uncertainty of the decision problem can be expressed as the conditional probability distributions shown in the tables below.
|
||||||
| Table 1: P(Oil). |
|
|||||||||||||||||||
|
Table 2: P(Seismic | Oil, Test=yes). |
|||||||||||||||||||
The profit (or loss) made by the Oil Wildcatter depends on the quality of the decision he makes. Solving the decision problem is a question of weighing the costs and rewards with the probability distributions specifying the uncertainty in the decision problem under the assumption that the decision maker tries to optimize the expected utility. The table below shows the expected cost and reward made by the Oil Wildcatter when he adheres to the (optimal) strategy identified by solving the influence diagram representation shown above.
Expected Cost and Reward
| Expected Utility | |
| Cost | |
| Reward | |
| Cost + Reward |
Hence, the expected utility of the decision scenario is .
The table below shows the probability distribution over the amount of oil at the site. The prior distribution is 50% dry, 30% wet and 20% soaking. The probability distribution changes when a test result is obtained.
Amount of Oil at site
| State | Probability | Expected Utility |
| Dry (no oil) | ||
| Wet (some oil) | ||
| Soaking (a lot of oil) |
The first decision considered by the Oil Wildcatter is whether or not to perform a seismic soundings test before deciding whether or not to drill.
Seismic Soundings Test Decision
The expected utility of the two decision options related to the seismic soundings test
| Test Option | Expected Utility |
| Perform Test | |
| Do Not Perform Test |
Enter the actual decision on the seismic soundings test below
| Seismic Soundings Test | |
| Seismic Soundings Test Result |
The second and last decision the Oil Wildcatter has to make is the Drill dection.
Drill Decision
The expected utilities of the two decision options related to the drill decision and the probabilities of making each decision under the (optimal) strategy identified are shown below. The latter is the probability of future decisions and changes as observations and decisions are made. Thus, initially there is 59% probability that the Oil Wildcatter will drill for oil.
| Drill Option | Expected Utility | Probability |
| Drill for Oil | ||
| Do Not Drill for Oil |
Enter the actual drill decision below (and see the expected utility in the table above)
| Drill decision |
